Basic Probability Proof

Purpose: This is a basic proof of probability of two events, just in case you were wondering. I will show the proof of why you multiply the numerators and denominators.

Let









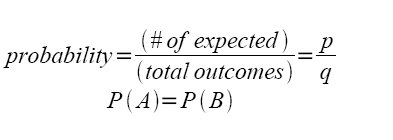
Formula:








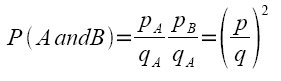
Proof:

We are dealing with two events.

Probability means total expected(desired) outcomes over total outcomes.

only expected outcomes -----------> pA(1st) pB(2nd)
total outcomes --------------------->qA(1st) qB(2nd)

Count them up!




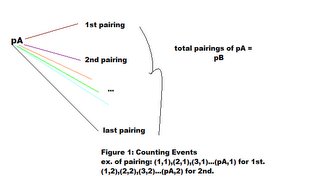
(Enlarge diagram by clicking it)







Figure 1 reflects the well-taught Counting Principle, which just means to multiply for deducting totals.

All possible pA and pB events = pA [1st pairing] + pA [2nd pairing] + ... pA [last pairing] =
( pB [total pairings] )( pA) = pA * pB

Similarly,

Total outcomes = qA * qB

This proves P(A and B) = (pA *pB) / (qA * qB).

Quick Discussion:

Common misconception is to add two independent events, but you can't because they are separate.

Ex. Let P(A) = 9/10 and P(B) = 3/10. Adding gives you 6/5. The numerator cannot go over the denominator.

Total probability never exceeds one!